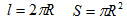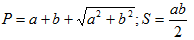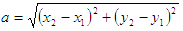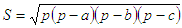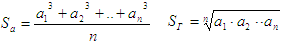|
Программы обучения:
Группа А (уровень Basis - базовый,
7-9 класс) подробнее>>
Группа B (уровень ProA - продвинутый уровень А, 8-10 класс) подробнее>>
Группа C (уровень ProB - продвинутый уровень B, 9-11 класс) подробнее>>
|
 |
|
|
Задачи (1-8) и тесты для тренировки 1а >>
Задачи (9-16) и тесты для тренировки 1b >>
Задачи (16-24) и тесты для тренировки 1c >>
Для решения задач можно использовать тестовую систему
evrika.nov.ru.
Для теоретической справки материал сайта дистанционной подготовки по информатике
http://informatics.mccme.ru
Тренировка №1a: "Следование" (a-01a.doc)
№1. Сумма, разность, произведение и частное
Даны два числа a и b. Вычислить их сумму,
разность, произведение и частное.
Входные данные:
В первой строке записаны действительные числа a и b (по модулю не превышают 1000, b не равно 0).
Выходные данные:
Четыре числа с точностью до второго знака: сумма, разность, произведение и частное.
Числа в одной строке и разделенные пробелом.
Пример.
на входе:
3 4
на выходе:
7.00 -1.00 12.00 0.75
|
№2. Площадь круга и длина окружности
Вычислить площадь круга и длину окружности одного и того же
заданного радиуса R
Примечание: формулы длины окружности и площади
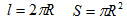
Входные данные:
В первой строке записан радиус R (0 < R ≤ 109).
Выходные данные:
Два числа в одной строке разделенные пробелом с точностью до второго знака:
площадь круга и длина окружности.
Пример.
на входе:
4.0
на выходе:
50.27 25.13
|
Скачать Zip-файл для этой задачи >>
| |
№3. Куб
Дана длина ребра куба. Найти площадь грани, площадь полной поверхности
и объем этого куба.
Входные данные:
В первой строке записано не отрицательное действительное число (по модулю
не превышает 1000) - длина ребра куба.
Выходные данные:
Три числа с точностью до второго знака: площадь грани, площадь поверхности
куба, объем куба.
Числа в одной строке и разделенные пробелом.
Пример 1.
на входе:
3
на выходе:
9.00 54.00 27.00
Пример 2.
на входе:
0.5
на выходе:
0.25 0.15 0.13
|
№4. Треугольник
Вычислить периметр и площадь прямоугольного треугольника
по заданным длинам двух катетов а и b.
Примечание: формулы вычисления периметра и площади
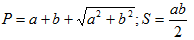
Входные данные:
В первой строке записаны два не отрицательных действительных числа (по модулю
не превышают 32000) - катеты прямоугольного треугольника.
Выходные данные:
Два числа с точностью до второго знака: периметр и площадь треугольника.
Числа в одной строке и разделенные пробелом.
Пример 1.
на входе:
3 4
на выходе:
6.00 12.00
Пример 2.
на входе:
2 5
на выходе:
5.00 12.39
|
№5. Расстояние между точками
Вычислить расстояние между двумя точками с данными
координатами (х1, у1), (x2, у2).
Примечание: расстояние между точками вычисляется по формуле
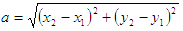
Входные данные:
В первой строке записано четыре действительных числа (по модулю
не превышает 1000) - координаты точек (первое число х1 - координата "х" первой точки,
второе число y1 - координата "y" первой точки, третье число х2 -
координата "х" второй точки и четвертое число y2 - координата "y" второй точки.
Выходные данные:
расстояние между точками с точностью до второго знака.
Пример 1.
на входе:
0 0 0 3
на выходе:
3.00
Пример 2.
на входе:
-2 -2 -2 3
на выходе:
5.00
|
№6. Произведение цифр
Найти произведение цифр заданного четырехзначного числа.
Входные данные:
В первой строке записано четырехзначное число.
Выходные данные:
Произведение цифр заданного числа.
Пример 1.
на входе:
1234
на выходе:
24
Пример 2.
на входе:
7582
на выходе:
560
|
№7(дополнительная). Треугольник 2
Заданы координаты трех вершин треугольника: (х1, у1), (x2, у2), (x3, y3).
Найти его периметр и площадь.
Примечание: площадь вычисляется по формуле Герона, где p - полупериметр
треугольника
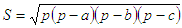
Входные данные:
В первой строке записано шесть вещественных чисел (не превышают 10 000 по
модулю) - координаты вершин треугольника.
Выходные данные:
Площадь и перимерт треугольника. Числа с точностью до второго знака после
запятой, разделены пробелом.
Пример 1.
на входе:
0 0 0 3 4 0
на выходе:
6.00 12.00
Пример 2.
на входе:
1 1 3 3 3 1
на выходе:
2.00 6.82
|
№8(дополнительная). Два числа
Даны два числа. Найти среднее арифметическое кубов этих чисел и среднее
геометрическое модулей этих чисел.
Примечание: для n чисел среднее арфметическое кубов и
среднее геометрческое модулей вычисляется по формуле
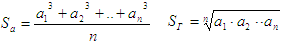
Входные данные:
В первой строке записано два вещественных числа (не превышают 1000 по модулю).
Выходные данные:
Среднее арифметическое кубов и среднее геометрическое модулей заданных чисел.
Числа с точностью до второго знака после запятой, разделены пробелом.
Пример 1.
на входе:
2 7
на выходе:
175.50 3.74
Пример 2.
на входе:
36 42
на выходе:
60372.00 38.88
|
Тренировка №1b: "Следование" (a-01b.doc)
№1(9). Равносторонний треугольник
Дано число a - сторона равностороннего треугольника.
Найти площадь этого треугольника, его высоту, радиус
вписанной и описанной окружностей.
Примечание: формулы описанной и вписанной окружности, площадь треугольника, высота
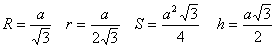
Входные данные:
Вещественное число a (a < 109) - сторона треугольника.
Выходные данные:
числа являющиеся ответом в соответствии с условием задачи с
точностью до третьего знака после запятой. Числа разделены пробелом.
Первое число площадь треугольника, второе - его высота, третье - радиус
вписанной окружности, четвертое число - радиус описанной окружности.
Пример 1.
на входе:
1
на выходе:
0.433 0.866 0.289 0.577
Пример 2.
на входе:
1000000
на выходе:
433012701892.219 866025.404 288675.135 577350.269
|
Скачать Zip-файл для этой задачи >>
| |
№2(10). Площадь круга
Известна длина окружности L. Найти S площадь круга,
ограниченного этой окружностью.
Входные данные:
одно вещественное число L
Выходные данные:
число являющееся ответом на условие задачи.
Пример 1.
на входе:
10
на выходе:
7.95775
Пример 2.
на входе:
6.28
на выходе:
3.13841
Пример 3.
на входе:
101010
на выходе:
811930541.69048
|
Скачать Zip-файл для этой задачи >>
| |
№3(11). Площадь кольца
Найти площадь кольца, внутренний радиус которого равен 4, а внешний - заданному числу R.
Входные данные:
одно вещественное число R, (R>4)
Выходные данные:
число являющееся ответом на условие задачи.
Пример 1.
на входе:
5
на выходе:
28.274
Пример 2.
на входе:
4.1
на выходе:
2.545
Пример 3.
на входе:
7234
на выходе:
164401868.341
|
Скачать Zip-файл для этой задачи >>
| |
№4(12). Корни квадратного уравнения
Вычислить корни квадратного уравнения
ax2 + bx + с = 0, заданного коэффициентами а, b и с
(предполагается, что дискриминант
уравнения неотрицателен).
Входные данные:
три вещественных числа a, b, c - коэффициенты уравнения
(а <> 0).
Выходные данные:
два числа являющиеся ответом в соответствии с
условием задачи.
Пример 1.
на входе:
1 2 1
на выходе:
-1.00 -1.00
Пример 2.
на входе:
-5 6 3
на выходе:
-0.38 1.58
Пример 3.
на входе:
1 5 0
на выходе:
0.00 -5.00
|
Скачать Zip-файл для этой задачи >>
| |
№5(13). Оптимизация вычислений
Дано действительное число х. Не пользуясь никакими
другими арифметическими операциями, кроме умножения,
сложения и вычитания, вычислить за минимальное число
операций 2х4 - Зх3 + 4х2 - 5х + 6.
Входные данные:
одно вещественное число x
Выходные данные:
число являющееся ответом на условие задачи.
Пример 1.
на входе:
10.3
на выходе:
19610.8552
Пример 2.
на входе:
-9
на выходе:
15684.0000
Пример 3.
на входе:
-0.2
на выходе:
7.1872
|
Скачать Zip-файл для этой задачи >>
| |
№6(14). Перевод температур
Известно значение температуры по шкале Цельсия.
Найти соответствующие значения температуры по шкалам Фаренгейта
и Кельвина, Известно, что для пересчета по шкале Фаренгейта
нужно исходное значение t°С умножить на 1,8 и прибавить 32,
а по шкале Кельвина значение абсолютного нуля
соответствует -273,15°С.
Входные данные:
одно вещественное число - температура по шкале Цельсия
Выходные данные:
два вещественных числа являющиеся ответом
в соответствии с условием задачи, с точностью
до второго знака разделенные пробелом.
Пример 1.
на входе:
10.3
на выходе:
50.54 283.45
Пример 2.
на входе:
-25
на выходе:
-13.00 248.15
Пример 3.
на входе:
0
на выходе:
32.00 273.15
|
Скачать Zip-файл для этой задачи >>
| |
Назад >>
Координатор проекта "Компьютерная Школа" Иванов Андрей Николаевич.
Вы можете послать свое сообщение по электронному адресу temp3@yandex.ru
или посетить раздел Контакты.
|